Processing math: 100%
Up 気圧モデル 作成: 2022-07-26
更新: 2023-09-07

    風船を手で潰そうとしても，潰れない (せいぜい風船を破裂させるくらい)。
    潰す力に抵抗しているのは，風船の中の空気の存在である。
    ゴム膜で覆った鉄をを手で潰そうとしても，潰れない。
    潰す力に抵抗しているのは，ゴム膜の中の鉄の存在である。

    しかし，潰れない理由の立て方が，空気の場合は特殊である。
    即ち，以下に示す理屈を立てる。


    ウォーミングアップ
    データ :「空気は，窒素 (分子量 28) 80%，酸素 (分子量 32) 20% の組成」
    よって，
      「空気の分子量」＝ 28 × 0.8 + 32 × 0.2 ＝ 28.8
    アボガドロ数を
      NA = 6.02 ×1023
    とすると，
      「空気分子の質量」= 28.8 ÷ NA = 4.78 x 10−23 グラム

    データ : 「1モルの気体の体積は，常温 (0°C) 常圧 (1013 hPa) で約 22.4リットル = 0.0224 m3」(Wikipedia「モル体積」)
    よって，つぎは「常温常圧の空気」の状態：
      「体積 0.0224 m3 の立方体の箱の中に，空気分子が１モル存在」


    空気分子の運動速度と空気圧の計算
    文字を M,m,V,a を，つぎのように措く：
      M = 空気 １mol の重さ = 0.0288 [kg]
      ｍ ＝ 空気分子の質量 [kg]
      V ＝ 空気 1mol の体積 = 0.0224 [m3]
      a = 体積が V の立方体の１辺の長さ [m}

    空気分子は，ランダムに飛び交っている。
    空気分子の速度ベクトルを，箱の３組の対面方向 (x, y, z 方向) 成分に分ける。
    そして，＜空気分子が壁に衝突＞が壁に与える圧力を，x方向で対面する２つの壁のうちの１つＳで考える。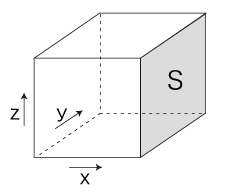


    分子のｘ方向の速さを vx m/s とする。
    分子は，Ｓ→対面の壁→Ｓ の移動に 2a/vx 秒かかる。
    これは分子１個がＳと，毎秒 vx/2a 回衝突するということ。
    箱の中の分子すべてでは，毎秒 NA vx/2a 回の衝突。

    分子１個の衝突がＡに与える力は？
    Ｓが受けるこの力は，力積で考えるとしている。
    この力積は，衝突による分子の運動量の変化量と等価。
    その変化量は：
      mvx−(−mvx)=2mvx
    よって，全分子の毎秒 NA vx/2a 回の衝突は，Ｓに毎秒つぎの力を与える：
      (2mvx)(NA vx/2a)=mNA vx2/a=Mvx2/a
    これの m平方あたりの力──圧力 p ──は，
      p=(Mvx2/a)/a2=Mvx2/a3=MVvx2 [Pa]

    変形して，
      pV=Mvx2

    この式の左辺に，理想気体の状態方程式
      pV=nRTR=8.31[Jmol⋅K]
    の右辺を代入する。
    いまは，
      n=1 [mol]T=273 [K]
    の設定なので，つぎのようになる：
      RT=Mvx2vx=√RTM=√8.31×2730.0288=281[m/s]

    また，
      pV=nRTV=0.0224 [m3]
    から，
      p=RTV=8.31×2730.0224=101278[Pa]=1013[hPa]


    「地上の気圧の実際値とドンピシャリ！気圧モデルは正しい！」と思わないこと。
    ドンピシャリなのは，ドンピシャリになるように R の値を決めているからである。
    上の計算は，トートロジーをやっているのである。

    さて，あなたはこの「気圧モデル」を受け入れるかな＾＾