電磁気学はいろいろなベクトル場を考えることになり,rotation はその各ベクトル場に対し適用され得るものになる。 ここでは,rotation の意味を,rot→E の場合で説明する。 rot→E の大意は,つぎのようになる:
ポテンシャルの損得」 rotation の概念は,わかりにくい。 わかりにくいのは,つぎの二点による: 即ち,rot→E は,つぎのように定義される: 以下,この概念がつくられるロジックを見ていく。 電場 →E(→x) の中の微小面積 dS を考える: 
単位電荷が dS の縁を一周するときの仕事を,dW とする。 そして「単位面積あたりの仕事」に dW を換算したものを,W とする。 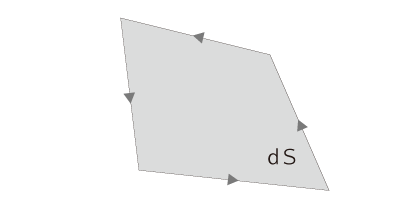
dS を,yz平面,zx平面,xy平面それぞれに射影する:
dSy : zx平面への射影 dSz : xy平面への射影 仕事 dWx,dWy,dWz をつぎのように定める:
dWy : 単位電荷が dSy の縁を一周するときの仕事 dWz : 単位電荷が dSz の縁を一周するときの仕事 dWx,dWy,dWz をそれぞれ「単位面積あたりの仕事」に換算したものを,Wx,Wy,Wz とする。 このとき,W はベクトル (Wx,Wy,Wz) の大きさと等しい。 以下,(Wx,Wy,Wz) を求める。 Wx の場合: はじめに,dSx が長方形の場合を考える: 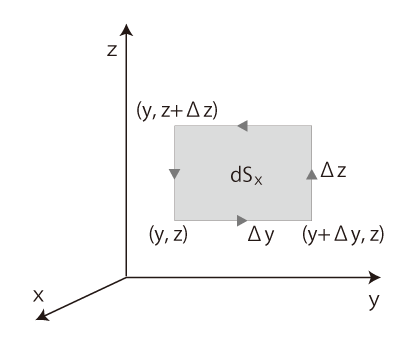
このとき,
dSx の一般形に対しては,つぎの区分求積を考える: 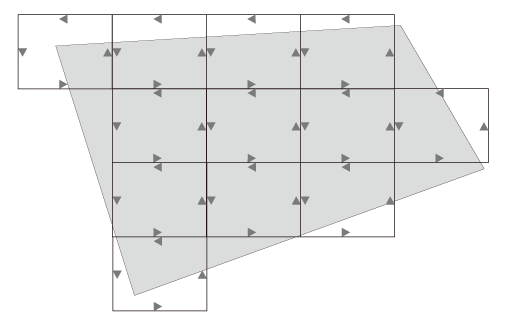
区分した長方形の辺長を Δy1,Δz1 とし,これの一周の仕事を dWx1 とする。 重なる辺で仕事が相殺されるので,つぎが成り立つ:
dWx は面積 dSx あたりの仕事なので,
Wx の計算と同様に, Wy,Wz を計算する。 結果は,つぎのようになる: この式の右辺を,rot→E と表す: 演算子記号 ∇=(∂∂x,∂∂y,∂∂z) を用いれば,形式的に →E=(Ex,Ey,Ez) との外積ということになる:
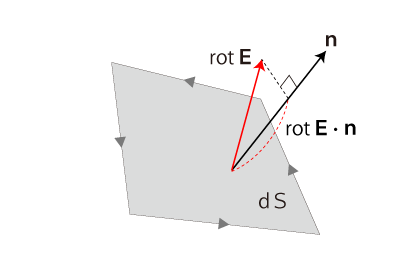
|