Up

自転軸系経度緯度と公転軸系直交座標の変換式

作成: 2020-09-05 更新: 2020-09-25

---

問題 公転軸系直交座標が (ｘ, y, z ) の地点Ｐの自転軸系経度緯度は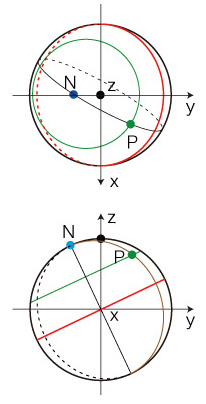？ Ｐの緯度，経度を，それぞれａ, ｂとする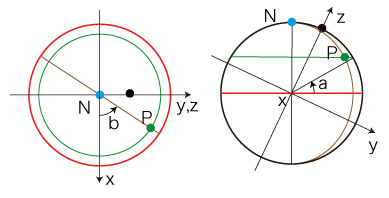： ベクトルｕ, ｖ, ｗ を，つぎのようにとる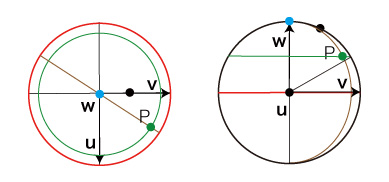： Ｐの位置ベクトルをｘ とするとき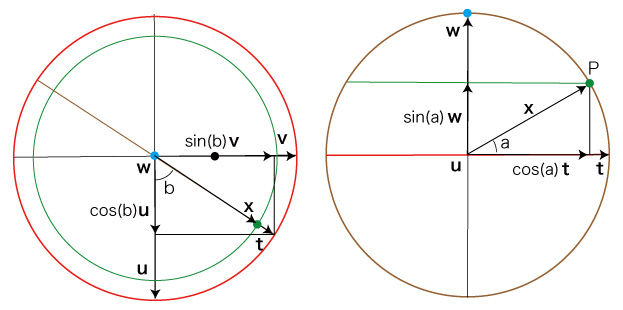， \[ \begin{align} {\bf x} &= cos(a) {\bf t} + sin(a) {\bf w} \\ &= cos(a) ( cos(b) {\bf u} + sin(b) {\bf v} ) + sin(a) {\bf w} \\ &= cos(a) cos(b) {\bf u} + cos(a) sin(b) {\bf v} + sin(a) {\bf w} \\ \ \\ \end{align} \] このベクトルの方程式を，座標の方程式に書き換える。 以下，つぎの略記を用いる： \[ \begin{align} n_s = sin(n), &\quad n_c = cos(n) \\ a_s = sin(a), &\quad a_c = cos(a) \\ b_s = sin(b), &\quad b_c = cos(b) \\ \ \\ \end{align} \] ｕ, ｖ, ｗ の座標は： \[ {\bf u} = (1, 0, 0) \\ {\bf v} = (0, cos(n), sin(n)) \\ {\bf w} = (0, -sin(n), cos(n)) \\ \] 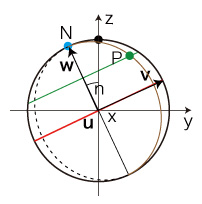よって， \[ \begin{align} (x, y, z) &= a_c b_c(1, 0, 0) + a_c b_s (0, n_c, n_s) + a_s (0, -n_s, n_c) \\ &= (a_c b_c, 0, 0) + (0, a_c b_s n_c, a_c b_s n_s) + (0, - a_s n_s, a_s n_c) \\ &= (a_c b_c, \ a_c b_s n_c - a_s n_s, \ a_c b_s n_s + a_s n_c) \\ \end{align} \] \[ \begin{align} \Longrightarrow \ &x = a_c b_c \\ &y = n_c a_c b_s - n_s a_s \\ &z = n_s a_c b_s + n_c a_s \\ \end{align} \\ \ \\ \] この式から，逆に ａ, ｂを x, y, z で表す。 \( x = a_c b_c, \ y = n_c a_c b_s - n_s a_s \) に \[ a_c = \sqrt{1-(a_s)^2} \\ b_c = \pm \sqrt{1-(b_s)^2} \\ \] を代入： \[ x = \pm \sqrt{1-(a_s)^2} \sqrt{1-(b_s)^2} \\ y = n_c \sqrt{1-(a_s)^2} b_s - n_s a_s \\ % z = \pm n_s \sqrt{1-(a_s)^2} b_s + n_c a_s \\ \ \\ \begin{align} \Longrightarrow \ & x^2 = (1-(a_s)^2) (1-(b_s)^2) \\ & (y + n_s a_s)^2 = (n_c)^2 (1-(a_s)^2) (b_s)^2 \\ % (z - n_c a_s)^2 = (n_s)^2 (1-(a_s)^2) (b_s)^2 \\ \ \\ \Longrightarrow \ & (b_s)^2 = 1- \frac{x^2}{1 - (a_s)^2} = \frac{(y + n_s a_s)^2}{(n_c)^2 (1-(a_s)^2)} % = \frac{(z - n_c a_s)^2}{(1-(n_s)^2) (1-(a_s)^2)} \end{align} \] これを，\(a_s\) の方程式として解く： \[ \begin{align} \Longrightarrow \ & (n_c)^2 (1-(a_s)^2) - (n_c)^2 x^2 = (y + n_s a_s)^2 \\ \ \\ \Longrightarrow \ & - (n_c)^2 \ (a_s)^2 + (n_c)^2 (1 - x^2) = y^2 + 2 n_s y a_s + ( n_s a_s)^2 \\ \ \\ \Longrightarrow \ & (( n_s)^2 + (n_c)^2) (a_s)^2 + 2 \ n_s \ y \ a_s - (n_c)^2 (1 - x^2) + y^2 = 0 \\ \ \\ \Longrightarrow \ & (a_s)^2 + 2 \ n_s \ y \ a_s - (n_c)^2 (1 - x^2) + y^2 = 0 \\ \ \\ \Longrightarrow \ & a_s = - n_s \ y \pm \sqrt{ (n_s \ y)^2 + (n_c)^2 (1 - x^2) - y^2 } \\ & \quad = - n_s \ y \pm \sqrt{ (n_c)^2 (1 - x^2- y^2) } \\ & \quad = - n_s \ y \pm n_c \ z \\ \end{align} \] \( - n_s \ y \pm n_c \ z \) に \[ y = n_c a_c b_s - n_s a_s \\ z = n_s a_c b_s + n_c a_s \] を代入すると \[ - n_s \ y \pm n_c \ z \\ \quad = - n_s (n_c a_c b_s - n_s a_s) \pm n_c (n_s a_c b_s + n_c a_s) \\ \quad = - n_s n_c a_c b_s + (n_s)^2 a_s) \pm ( n_s n_c a_c b_s + (n_c)^2 a_s ) \] これが \( a_s \) と等しくなるのは，「\( \pm \)」が「＋」の場合。 よって， \[ a_s = - n_s \ y + n_c \ z \\ \ \\ \] さらに \[ \begin{align} b_c &= \frac{x}{a_c} \\ &= \frac{x}{ \sqrt{ 1 - (a_s)^2 } } \\ &= \frac{x}{ \sqrt{ 1 - ( - n_s \ y + n_c \ z )^2 } } \\ &= \frac{x}{ \sqrt{ 1 - ( (n_s)^2 y^2 - 2 n_s n_c y z + (n_c)^2 z^2 ) } } \\ &= \frac{x}{ \sqrt{ 1 - (n_s)^2 y^2 + 2 n_s n_c y z - (n_c)^2 z^2 } } \\ \end{align} \] まとめ \[ x = a_c b_c \\ y = n_c a_c b_s - n_s a_s \\ z = n_s a_c b_s + n_c a_s \\ \\ \ \\ n_s \ y - n_c \ z + a_s = 0 \\ \ \\ a_s = - n_s \ y + n_c \ z \\ b_c =\frac{x}{ \sqrt{ 1 - (n_s)^2 y^2 + 2 n_s n_c y z - (n_c)^2 z^2 } } \\ \ \\ \]