Up 「式」「変わり方」が,「関数」の捉えになっている 作成: 2009-01-29
更新: 2011-04-14

    関数の始集合と終集合がともに「要素の変位」を考えられるような空間である場合，つぎのように，この関数に「変位の対応」を読むことができる：



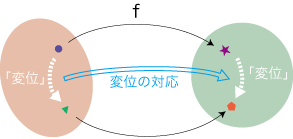
    ユークリッド空間は，「要素の変位」を視覚的に表せすことのできる空間である。
    例えばつぎは，比例関数のグラフに「変位の対応」を読んでいる場合であるが，ここでｘ軸，y軸は１次元ユークリッド空間として扱われていることになる：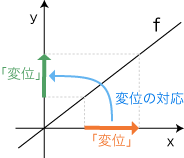



    「変位の対応」が対象になるためには，関数の定義である「一意対応」にいろいろ条件をつけることが必要になる。
    しかし学校数学では，この「変位の対応」を「変わり方」の話にして，「関数とは変わり方のことだ」みたいに「関数」を指導している。

    学校数学の「関数」は，「一意対応」ではない。
    数学でも，「関数」は「変わり方」として始まった。 「関数」の定義が「一意対応」になったのは，ずっと後になってからのことである。

    ＜シンプル＞は，いつも最後に得られる。 そして＜シンプル＞を得たとき，これまでを振り返って，「いままではなんてグチャグチャな考え方をしていたんだ！」という見方ができるようになる。

    学校数学の「関数」は，「一意対応」になる前の「関数」(18, 19世紀の「関数」) である。 論理的にグチャグチャしている。
    したがって，論理にこだわるタイプの生徒には，受け付けられないものになっている。
    　 例：「変数」の意味が論理的に示されないまま。
    　　「ｙ」が「関数」と呼ばれる。

    生徒の「関数」の成績が悪いという事実に対しては，
      「関数という主題は，生徒にとって難しい。」
    というふうにではなく，先ず，
      「学校数学の関数は，論理に堪えない。
      　──論理に目をつぶらないと飲み込めない。      」
    というふうに思うべきである。