Up 「テンソル」の数学 :「テンソル積」 作成: 2018-01-23
更新: 2018-02-25

    「テンソル」は，数学から出て来たのではない。
    計算形式のあるものが「テンソル」と呼ばれてきたという経緯が，先ずある。
    数学は，「テンソル」を数学的に定式化して，「テンソル」の数学をつくる。

    この定式化は，「テンソル」と呼ばれてきたもの全体を収納するものとはなっていない。 即ち，「テンソル」と呼ばれてきたものには，この定式化からはじかれるものがある。
    例えば，「テンソル」といえば必ず主題になる「計量テンソル」は，この定式化から外れる。


    数学の「テンソル」は，簡単にいうと，記号「\(\otimes\)」の文法──「テンソル積」──である。
    その数学がどんなものかを，はじめに見ておく。


    つぎのように措く：
      \( U,\, V,\, W\) : 体 \(K\) 上のベクトル空間
      \( \phi \) : \(U \times V\) から \(W\) への双線型写像

    「長方形の面積」が最も卑近な例になるので，これをイメージにもつとよい：
    　　\( U\) : タテ(長さ) 全体
    \( V\) : ヨコ(長さ) 全体
    \( W \) : 面積全体
    \( \phi \) : (タテ \({\bf x}\), ヨコ \({\bf y}) \longmapsto\) タテ \({\bf x}\), ヨコ \({\bf y}\) の長方形の面積
    \(\phi\) は，タテ，ヨコの一方を固定したとき線型写像である：
    　　 タテの長さが２倍，３倍，‥‥ になれば，長方形の面積も２倍，３倍，‥‥ になる。
    ヨコについても同じ。
    この「一方を固定したとき線型」を，「双線型」というのである。


    つぎは，集合 \(U \times V\) 上の同値関係になる：
      \[ ({\bf x},\,{\bf y}) \sim ({\bf x'},\,{\bf y'}) \ :\ \phi({\bf x},\,{\bf y}) = \phi({\bf x'},\,{\bf y'}) \]
    この同値関係による \(U \times V\) の商集合を「\(U \bigotimes V\)」で表す。
    また，\( ({\bf x},\,{\bf y})\) が代表元になる同値類を，「\({\bf x} \otimes {\bf y}\)」で表す。

    「長方形の面積」の場合，「\(U \bigotimes V\)」は「タテ\(\bigotimes\)ヨコ」である。
    これは，長方形の面積が同じになる (タテ, ヨコ) の類別である。
    そして，例えば「タテ３cm，ヨコ４cm」と「タテ２cm，ヨコ６cm」は，長方形の面積が同じになるから，「３cm \(\otimes\)４cm = ２cm \(\otimes\)６cm」となる。


    \(U \bigotimes V\) は，体 \(K\) 上の線型空間になる。
    そして，最後の仕上げが，つぎの図式を可換にする線型写像 \(\bar{\phi} \) である :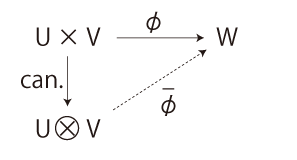
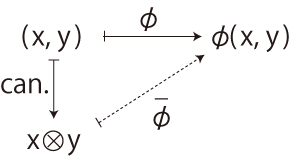
      要素の対応で書くと：

      ここで「can.」は, 「標準写像 canonical map」の意味。


    \(\bar{\phi} \) は，「長方形の面積」の例だと，「公式 : タテ × ヨコ ＝ 面積」と解釈されるものになる。
    実際，「\(\bar{\phi} \) : タテ\(\otimes\)ヨコ \( \longrightarrow \) 面積」に対しては，このように読むのみである。

    ここに，「計算公式」を身分とする数学的対象が得られたことになる。
    そして「テンソル」がこのときの手法がであったことから，「計算公式」は「テンソル」と関係していることが予想される。
    実際，「計算公式とはテンソルのことだ」が，結論として用意されているものである。


    計算公式が「計算公式」である所以は，量計算式の場合だと「単位を変えても形式が保たれる」である。
    そこで，一般に計算公式が「計算公式」である所以は，「座標を変えても形式が保たれる」である。

    「座標を変えても形式が保たれる」がどうして要点になるのか？
    それは，「存在は表現に先立つ」の存在論に立つからである。
    「公式」には，「存在」を直接指すものとして，表現に依らないことが求められる。
    そして，「表現に依らない」の存在様式は，「形式」である。