「εテンソル」は,それである。 ϵijk が,つぎのように定義される:
「添字がついているからテンソルだ」の思いは,,
「ϵ テンソル」の ϵijk は,つぎの立方超行列の中に配置できる: 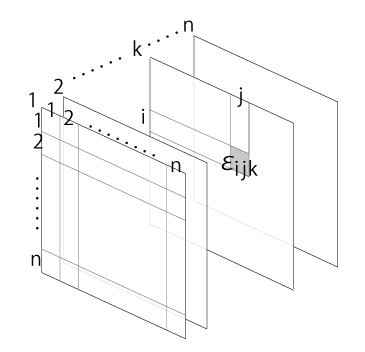
数学のテンソルは,「線型代数」の中の概念である。 εは,そうではない。 「εテンソル」は,偽テンソルである。 この方法を示しておく。 簡単のために,i,j,k∈{1,2,3} の場合で説明する。 集合 {1,2,3} を N , とおく。 そして,写像
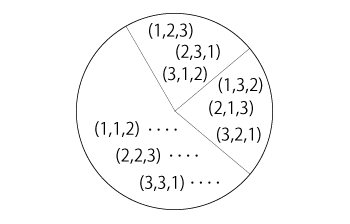
そしてこのとき,つぎの可換図式を得る: 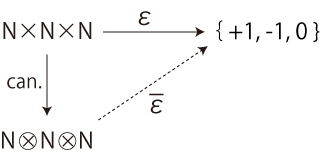
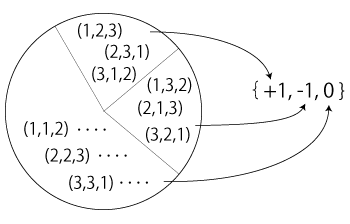
|
| Up | 「εテンソル」 | 作成: 2018-02-22 更新: 2018-02-22 |
「εテンソル」は,それである。 ϵijk が,つぎのように定義される:
「添字がついているからテンソルだ」の思いは,,
「ϵ テンソル」の ϵijk は,つぎの立方超行列の中に配置できる: 
数学のテンソルは,「線型代数」の中の概念である。 εは,そうではない。 「εテンソル」は,偽テンソルである。 この方法を示しておく。 簡単のために,i,j,k∈{1,2,3} の場合で説明する。 集合 {1,2,3} を N , とおく。 そして,写像

そしてこのとき,つぎの可換図式を得る: 

|