|
"量と測定" 教材の研究は, "ものごとの順番" として,量と数の概念ないしそれをめぐるひとの実践形態に対する (ある程度) 明確な把捉の後に続く。この把捉は,"量と測定" 教材研究の基礎研究として行なわれている必要がある。(勿論,これは "数と計算", "数量関係" の主題に対しても基礎研究として,引き継がれていく。)
量という実在(実体)があるわけではない。量は,ひとの読みとして起こる。そしてこの読みは,ことばの一つの論理系として収まる。 論理系としての量は,〈形式〉である。本論ではこれが,集合と構造のことばによって,1次元順序位相アフィン空間(Q, ( (D,+), (N,+,×), × ), +)として定式化される。ここで,Qの要素は "量(大きさ)",Dの要素は "量(大きさ)の差",そしてNの要素は "差の比" と,それぞれ読まれる。Nは一般的には実数体 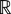 の部分体として意味づくが,現実にNとして考えるものは,有理数体 の部分体として意味づくが,現実にNとして考えるものは,有理数体 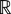 ないし実数体 ないし実数体 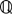 である。 である。
特に,ここでは,量(大きさ)そのものに対しては,内算法(加法)も数の倍の外算法も立たないというように考える。これらはQをDに埋め込むことで考えられるようになる,とする。 比は数に表現される。しかしこのように言うとき,数は,量とは別の文脈で対象として完結していなければならない。そして実際,数は,系列ないし計数("単位" の数え上げ)の文脈で対象として完結するのである。 《形式としての数は形式としての量と同じではない》という意味で,数は量ではない。しかし《数(集合)に量(形式)を与えることはできる》という意味で,数は量にもなる。(N, ( (N,+), (N,+,×), × ), +)がこのときの "量としての数" である。 |
|
( Abstracted ) As a ground-making for the study of "Quantities and Measurement" in elementary school mathematics, some fundamental concepts are studied ── mainly, the concepts of "quantit,y" and "number" themseIves . Quatities does not exist as actual beings. 'Ouantity' occurs as a reading that man practices. And this reading takes its place in a logical language system. Quantity-as-a-logical -system is a <form>. The author describes this by using the words of "set" and "structure" ── that i s, as a 1-dimensional ordered topological affine space ( Q, ( (D, +), (N, +, x), x ), +). Here the element of Q, that of D, and that of N are read "quantity(magnitude)", "difference of quantities", and "ratio of differences", respectively. N is usually understood as the field 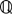 of rational numbers or the field of rational numbers or the field 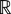 of real numbers. of real numbers.
Especially, here we don't think that the addition between quantities and the numeral multiplication of quantities are defined. We think these operations are defined when Q is considered embedded into D. Ratios are represented by numbers. But this way of expressing is possible when the number is completed in a context that is independent of the concept of quantity. In fact. the number is completed i n the context of "sequence" or "counting a unit". The number differs from the quantity in the sense that rumbers-as-forms differ from quantities-as-forms. But the number becomes quantity in the sense that we can give it the form of quantity. In fact., ( N, ( (N, +), (N, +, X), X ), + ) is a "number-as-quantity". |